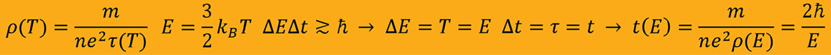This is the website of Timo Buttler. It is created for the reason:

In the years 2008-2009 I made my diploma thesis on experimental high-temperature superconductivity. While trying to understand the subject, I hit upon a new approach to explain superconductivity. But as a young diploma student, for the first time in contact with the real physical world, I was insecure, not knowing how to handle the situation. Due to this I didn't manage the new approach to get attention during my diploma thesis time at the university, which was the Technische Universität München. After I finished the thesis and left university, though, it was clear that I had to deal with it. And so, in the subsequent years, in my private time, I elaborated the approach into the work Solving the mystery of superconductivity by equating two equations. And, for the reason to publish it, this website is created. And, in addition to that, I created and started a Youtube channel in 2019. To present the work and its contents also in this way, with videos.

And here is a summary of the work:

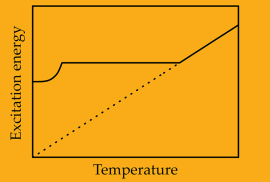
The basis of the new approach is that I think that there exists a lower limit for the excitation energy of a particle in certain systems. This is nothing new to physics in which similar limits exist for the velocity given by the speed of light or the ground state energy given by quantum mechanics. And, inspired by the possibility to compute the ground state energy with Heisenberg's uncertainty relation for position and momentum ΔxΔp≳ħ, I use the corresponding relation for energy and time ΔEΔt≳ħ to compute the minimum excitation energy. Where ΔE becomes the excitation energy E and Δt I choose to become the relaxation time t in which E is lost when the gain of energy disappears. And for the excitation-energy-dependent relaxation time t(E) I choose an expression not far from superconductivity, the phenomenon of vanishing electrical resistivity, namely, the central expression for the electrical resistivity, the Drude formula ρ(T)=m/ne^2τ(T). In it the temperature T can be identified with the excitation energy E via the equipartition relation and τ is a relaxation time which is why I choose τ(T) to become t(E). In this way the minimum excitation energy is computed

To maintain the excitation energy, which would otherwise decrease with decreasing temperature and disappear at absolute zero, I introduce an additional excitation energy which is called virtual. And this virtual excitation energy I think is, in turn, responsible for something fundamental in physics, the emergence of a new interaction. In case of electrons in a solid the superconducting interaction. Where I assume that the interaction takes place in the form that particles perform virtual relaxation processes in which virtual excitation energies, and corresponding virtual momenta, are lost and exchanged within virtual relaxation times and virtual relaxation paths. Also, this perspective suggests the explanation for the vanishing electrical resistivity that because electrons perform virtual relaxation processes they cannot perform real relaxation processes and so the relaxation time in the Drude formula goes to infinity. And hence, with the limited excitation energy and a temperature-dependent interaction one finds

Furthermore, this approach yields and predicts computable quantities which are in good agreement with the experiment. An impressive result is, for example, the formula for the critical magnetic field with the condition for type I superconductivity which simply relates the critical temperature to the Fermi temperature

A brief derivation of the formula is given in the work A formula for the critical magnetic field better than the BCS theory which also lists some of the other results in its appendix. Where the agreement is so good that it seems impossible that I didn't hit upon something big, something substantial. Yet naturally the approach is new and enters unknown territory which is why the elaboration of the approach into the work was challenging. Thus, it is surely the case that the elaborated views have, to a greater or a lesser extent, room for improvement. Nevertheless, I am sure that the thought is right. And that it is the basis for any theory of superconductivity and is thus the door that needed to be opened to the heart of superconductivity.

And, at the end, I have to comment on one circumstance. As said above, the relaxation time in the Drude formula I interpret as the period of time in which an electron loses its excitation energy. Where the excitation energy is the total one, constituting of the electric and the thermal excitation energy. In the Drude picture however, the relaxation time is interpreted as the period of time in which the drift velocity becomes zero, accordingly the period of time in which only the electric excitation energy is lost. The circumstance is now that if my interpretation of the relaxation time is used, which still can be seen to be consistent with the Drude picture and essentially completes it, it yields an explanation for the central law of electrical resistivity, published in the years 1826-1827, Ohm's law. Using the typical largeness of the thermal to the electric excitation energy to explain it. And additionally discussed in the work An explanation for Ohm's law.